[CF]Avito Cool Challenge 2018

A（签到）

题意：签到

00:01 1A

#include <bits/stdc++.h>

using namespace std;

typedef long long int LL;

#define st first
#define nd second
#define pb push_back
#define mp make_pair
#define pll pair <LL, LL>
#define pii pair <int, int>
#define rep(i,x) for(int i=1;i<=x;i++)

const int N = 1e5+7;
const int MX = 1e9+7;
const LL INF = 1e18+9LL;

int main(){
    int x;
    cin>>x;
    if(x==2)cout<<2;
    else cout<<1; 
}

View Code

B（构造）

题意：有长度为n的数列B，Ai表示B中与Bi不同的值的数量，给出数列A，求B

显然

1若Ai不同则Bi一定不同

2一定有n-Ai个数等于Bi

推出相同Ai的个数一定是n-Ai的倍数，其中每组n-Ai个Bi相等，否则无解，有解时方案按之前推论构造即可。

这题开始还没想出来，不应该。。

01:12 2A

#include <bits/stdc++.h>

using namespace std;

typedef long long int LL;

#define st first
#define nd second
#define pb push_back
#define mp make_pair
#define pll pair <LL, LL>
#define pii pair <int, int>
#define rep(i,x) for(int i=1;i<=x;i++)

const int N = 1e5+7;
const int MX = 1e9+7;
const LL INF = 1e18+9LL;

int a[N],sum[N],ans[N],lim[N];

vector<int> b[N]; 

int main(){
    int n;
    cin>>n;
    rep(i,n){
    scanf("%d",&a[i]);
    b[a[i]].pb(i);
    sum[a[i]]++;
    }
    for(int i=0;i<n;i++){
        if(sum[i]%(n-i)){
            cout<<"Impossible";
            return 0;
        }
        lim[i]=n-i;
    }
    cout<<"Possible"<<endl;
    int cnt=1;
    for(int i=0;i<n;i++){
        for(int j=0;j<b[i].size();j++){
            ans[b[i][j]]=cnt;
            if((j+1)%lim[i]==0)cnt++;
        }
    }
    rep(i,n)cout<<ans[i]<<" ";
    return 0;
}

View Code

C（dp）

题意：给n个方格涂m种颜色，有k个方格和左边的方格颜色不同，求方案数。（n<=2000,m<=2000）

f[i][j]=f[i-1][j]+(m-1)*f[i-1][j-1]，输出f[n][k]即可。数组可以滚动，但没必要。O(nk)

或者直接推公式也不难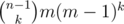 $\text{[math]}$

00:23 1A

#include <bits/stdc++.h>

using namespace std;

typedef long long int LL;

#define st first
#define nd second
#define pb push_back
#define mp make_pair
#define pll pair <LL, LL>
#define pii pair <int, int>
#define rep(i,x) for(int i=1;i<=x;i++)

const int N = 2e3+7;
const int MX = 1e9+7;
const LL INF = 1e18+9LL;
const LL mod=998244353;

LL dp[N][N];

int main(){
    int n,m,k;
    cin>>n>>m>>k;
    dp[0][0]=1;
    rep(i,n)
    for(int j=0;j<i&&j<=k;j++){
        if(j==0){
        dp[i][j]=m;
        continue;}
        dp[i][j]=((dp[i-1][j-1]*(m-1))%mod+dp[i-1][j])%mod;
    }
    cout<<dp[n][k];
}

View Code

D（MST）

题意：给出一个加权无向图，有k个特殊结点。定义路径长度为路径上的最大边权，求这k个结点到其他特殊结点最短路的最大值。

定义开始看起来很绕，后来一想其实类似货车运输。首先最短路一定在最小生成树上取到，观察样例可以猜想所有最大值相等。事实上，考虑kruskal算法过程，当一条边被加入时，如果他两边的并查集都含有特殊结点，那么答案一定不比这条边小，因为树上的路径唯一，两边的特殊结点间的路径一定包含这条边，据此也可发现所有结点的答案一定都相等。所以只需在kruskal执行时维护每个并查集的大小，当加入一条边后有一个并查集大小为k时，说明所有特殊结点已经联通，之后的边都不会影响答案，而当前加入的这条边一定连接了两个特殊结点，所以这条边的权值就是所有特殊结点的最大值。

比赛的时候没时间做了，想到了最小生成树，开始猜想最大值相等但是之后又想错了，主要还是开始理解题意耽误太多时间了。

#include <bits/stdc++.h>

using namespace std;

typedef long long int LL;

#define st first
#define nd second
#define pb push_back
#define mp make_pair
#define pll pair <LL, LL>
#define pii pair <int, int>
#define rep(i,x) for(int i=1;i<=x;i++)

const int N=1e5+7;

struct st  
{  
    int u,v,w;  
}edge[N];  

int f[N],ans[N],is[N],sz[N]; 

    int n,m,k;

int cmp(st a,st b){
    return a.w<b.w;
}

int finde(int x)  
{  
    if(x!=f[x])  
        f[x]=finde(f[x]);  
    return f[x];  
}  

int make(int a,int b)  
{  
    int x=finde(a);  
    int y=finde(b);  
    f[x]=y;  
    sz[y]+=sz[x];
    return sz[y]==k;
}  

int main(){ 

    scanf("%d%d%d",&n,&m,&k);
    rep(i,k){
        int x;
        scanf("%d",&x);
        is[x]=1;
    }
    rep(i,m)
    {  
    int a,b,c;
        scanf("%d%d%d",&a,&b,&c);  
        edge[i].u=a;  
        edge[i].v=b;  
        edge[i].w=c;  
    }  
    for(int i=1;i<=n;i++) {
        f[i]=i;  
        if(is[i])sz[i]=1;
    }
    sort(edge+1,edge+m+1,cmp);  
    rep(i,m)  
    {  
        int u=edge[i].u;  
        int v=edge[i].v;  
        if(finde(u)!=finde(v))  
        {   
            if(make(u,v)){
            rep(j,k)cout<<edge[i].w<<" ";
            return 0;
        }
        }  
    }  
    return 0;  
}

View Code

E（数学，构造）

题意：长度为n（n为偶数）的数列A的任意项前缀和为完全平方数，给出所有偶数项，求数列A，若有解保证存在1e13之内的解。（n<=1e5,Ai<=2e5）

令B_i为A的前i项和，令B_2*i=p^2，B_2*I-1=q^2，则A_2*i=p^2-q^2=(q+p)*(p-q)，显然p-q<sqrt(A_i)，因此枚举p-q的值，即可解出p和q。因为要保证B递增，所以要取使p最小的可行解，这样

之后的选择空间更大。O(n*sqrt(Ai))

02:19 3A

#include <bits/stdc++.h>

using namespace std;

typedef long long int LL;

#define st first
#define nd second
#define pb push_back
#define mp make_pair
#define pll pair <LL, LL>
#define pii pair <int, int>
#define rep(i,x) for(int i=1;i<=x;i++)

const int N = 1e5+7;
const int MX = 1e9+7;
const LL INF = 1e18+9LL;

LL ans[N],a[N];

int main(){
    int n;
    cin>>n;
    int cnt=0;
    rep(i,n/2){
        LL x;
        cin>>x;
        a[i*2]=x;
        LL j;
        for(j=sqrt(x);j>=1;j--){
        if(j*j==x)j--;
        if(!j)break;
        if(x%j==0&&(x/j-j)%2==0&&(x/j-j)/2>ans[cnt]){
        
        ans[++cnt]=(x/j-j)/2;
        ans[++cnt]=(x/j+j)/2;
        break;
        }
        }
        if(j==0){
        cout<<"No";
        return 0;
        }
    }
    
    cout<<"Yes"<<endl;
    LL now=0;
    for(int i=1;i<n;i+=2){
        cout<<ans[i]*ans[i]-now<<" "<<a[i+1]<<" ";
        now=ans[i+1]*ans[i+1];
    }
}

View Code

标答是O(Ai*log(Ai))的，还没仔细看，先贴这里。

Let $\text{[math]}$ , xmax = 2 × 105.

Since x2i = s2i - s2i - 1 = t2i2 - t2i - 12 ≥ (t2i - 1 + 1)2 - t2i - 12 = 2t2i - 1 + 1, so 2t2i - 1 + 1 ≤ xmax, t2i - 1 < xmax.

For every $\text{[math]}$ , we can precalculate all possible (a, b)s so that x = b2 - a2: enumerate all possible a 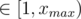$\text{[math]}$ , then for every a enumerate b from small to large starting from a + 1 and stop when b2 - a2 > xmax, record this (a, b) for x = b2 - a2. Since 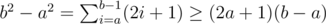$\text{[math]}$ , then 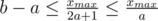$\text{[math]}$ , its complexity is $\text{[math]}$ .

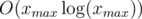Now, we can try to find a possible s from left to right. Since x2i - 1 is positive, we need to ensure t2i - 2 < t2i - 1. Becuase x2i = t2i2 - t2i - 12, we can try all precalculated (a, b)s such that x2i = b2 - a2. If we have several choices, we should choose the one that a is minimum possible, because if the current sum is bigger, it will be harder for the remaining number to keep positive.

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int,int> pii;
int n;
ll sq[100099];
#define S 200000
vector<pii> v[S+55];
int main()
{
    for(int i=1;i<=S;++i)
    {
        if(i*2+1>S) break;
        for(int j=i+1;j*(ll)j-i*(ll)i<=S;++j)
            v[j*(ll)j-i*(ll)i].push_back(pii(i,j));
    }
    scanf("%d",&n);
    for(int i=2;i<=n;i+=2)
    {
        int x; scanf("%d",&x);
        for(auto t:v[x])
            if(sq[i-2]<t.first)
            {
                sq[i-1]=t.first,sq[i]=t.second;
                break;
            }
        if(!sq[i-1])
        {puts("No"); return 0;}
    }
    puts("Yes");
    for(int i=1;i<=n;++i)
        printf("%lld%c",sq[i]*(ll)sq[i]-sq[i-1]
        *(ll)sq[i-1]," 
"[i==n]);
}