
一、从马尔科夫过程到Q学习
# 有一定基础的读者可以直接看第二部分
Q学习(Q-learning)算法是一种与模型无关的强化学习算法,以马尔科夫决策过程(Markov Decision Processes, MDPs)为理论基础。
标准的马尔科夫决策过程可以用一个五元组<S,A,P,R,γ> 表示,其中:
- S是一个离散有界的状态空间;
- A是一个离散的动作空间;
- P为状态转移概率函数,表示agent在状态s下选取动作a后转移到a’的概率;
- R为回报函数,用于计算agent由当前状态 选取动作 后转移到下一状态 得到的立即回报值,由当前状态和选取的动作决定,体现了马尔科夫性的特点;
- γ是折扣因子,用于确定延迟回报与立即回报的相对比例, 越大表明延迟回报的重要程度越高。
马尔科夫决策问题的目标是找到一个策略 ,使其回报函数 的长期累积值的数学期望
最大。其中,策略π只和状态相关,与时间无关(静态的)。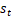
 是t时刻的环境状态,
是t时刻的环境状态, 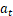
 是t时刻选择的动作。
是t时刻选择的动作。
根据Bellman最优准则,得到最优策略 对应的最优指标为:
其中, R(s,a)为r(st,at)的数学期望,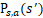
 为在状态s下选取动作a后转移到下一状态状态s’的概率。由于某些环境中状态之间的转移概率P不容易获得,直接学习
为在状态s下选取动作a后转移到下一状态状态s’的概率。由于某些环境中状态之间的转移概率P不容易获得,直接学习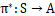
 是很困难的,而Q学习不需要获取转移概率P,因而可用来解决此类具有马尔科夫性的问题。
是很困难的,而Q学习不需要获取转移概率P,因而可用来解决此类具有马尔科夫性的问题。
Q学习是一种与环境无关的算法,是一种基于数值迭代的动态规划方法。定义一个Q函数作为评估函数:
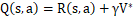

评估函数Q(s,a)的函数值是从状态s开始选择第一个动作a执行后获得的最大累积回报的折算值,通俗地说,Q值等于立即回报值r(s,a) 加上遵循最优策略的折算值,此时的最优策略可改写为:
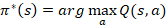

该策略表达式的意义在于:如果agent用Q函数代替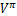
 函数,就可以不考虑转移概率P,只考虑当前状态s的所有可供选择的动作a,并从中选出使Q(s,a)最大的动作,即agent对当前状态的部分Q值做出多次反应,便可以选出动作序列,使全局最优化。
函数,就可以不考虑转移概率P,只考虑当前状态s的所有可供选择的动作a,并从中选出使Q(s,a)最大的动作,即agent对当前状态的部分Q值做出多次反应,便可以选出动作序列,使全局最优化。
在Q学习中,agent由初始状态转移到目标状态的过程称为“Episode”,即“场景”。Q函数可以表示为以下的迭代形式进行Q矩阵的更新:
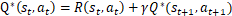

在每一步的迭代中,上式又可写为:
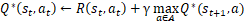

即Q矩阵(st,at)位置元素的值等于回报函数R的相应值加上折扣因子γ乘以转换到下一个状态后最大的Q值。
上述的Q学习算法可以看出,当划分的状态有限时,每一场景开始时随机选择的初始状态s在算法的指导下探索环境,最终一定可以到达目标状态s*,回报函数R(s,a)是有界的,并且动作的选择能够使每个状态映射到动作对的访问是无限频率,则整个学习过程就能够训练出来。
Q学习通过对环境的不断探索,积累历史经验,agent通过不断试错来强化自身,最终可以达到自主选择最优动作的目标,即不论出于何种状态,都可给出到达目标状态的最优选择路径,该算法中环境和动作相互影响,动作的选择影响环境状态,环境也可以通过强化回报函数 来反馈动作的优劣性,影响动作的选择。
参考文献:
[1]汪黎明.制造企业零库存管理物资调度方法研究[J].价值工程, 2019,38(23):126-129.
二、由一个广为流传的小例子了解Q学习的算法逻辑
一个由门连接的建筑物中有五个房间,如下图所示,分别用0-4号标识,将外界看作一个大房间,同样标识为5。
每个房间代表一个节点,门代表连线,可以将上图抽象为下面这样:

agent会被随机放置在任意一个房间里,然后从那个房间出发,一直走到建筑外(即5号房间为目标房间)。门是双向的,所以相邻节点间是双向箭头连接。通过门可以立即得到奖励值100,通过其他门奖励值为0。将所有箭头标注奖励值如下图:
在Q学习中,目标是达到奖励最高的状态,所以如果agent到达目标,它将永远在那里。 这种类型的目标被称为“吸收目标”。
想象一下,我们的agent是一个想象的虚拟机器人,可以通过经验学习。 agent可以从一个房间转移到另一个房间,但它没有上帝视角,也不知道哪一扇门通向外面。
按照第一部分Q学习的理论,我们把每个房间抽象为一个状态,选择进入哪号房间作为动作,把状态图和即时奖励值放到下面的奖励值表“回报矩阵R”中:(-1表示不可选择的动作,两个状态间没有连接)
现在我们将添加一个类似的矩阵“Q”给我们agent的大脑,代表了通过经验学到的东西的记忆。 矩阵Q的行表示agent的当前状态,列表示导致下一个状态的可能动作(节点之间的连线)。
agent开始什么都不知道,矩阵Q被初始化为零。 在这个例子中,为了解释简单,我们假设状态的数目是已知的(六个,0-5)。 如果我们不知道涉及多少个状态,矩阵Q可能从只有一个元素开始。 如果找到新的状态,则在矩阵Q中添加更多的列和行是一项简单的任务。
Q学习的更新规则如下:
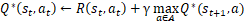

根据这个公式,分配给矩阵Q的特定元素的值等于矩阵R中相应值加上学习参数γ乘以下一状态下所有可能动作的Q的最大值。
每一场景的探索都会为agent增加经验,Q矩阵得到更新。训练的基本思路如下图:
基于算法思想,训练Q矩阵的具体流程如下:
步骤1.初始化仓库环境和算法参数(最大训练周期数,每一场景即为一个周期,折扣因子γ,即时回报函数R和评估矩阵Q。)。
步骤2.随机选择一个初始状态s,若s=s*,则结束此场景,重新选择初始状态。
步骤3.在当前状态s的所有可能动作中随机选择一个动作a,选择每一动作的概率相等。
步骤4.当前状态s选取动作a后到达状态s’。
步骤5.使用公式对Q矩阵进行更新。
步骤6.设置下一状态为当前状态,s=s‘。若s未达到目标状态,则转步骤3。
步骤7.如果算法未达到最大训练周期数,转步骤2进入下一场景。否则结束训练,此时得到训练完毕的收敛Q矩阵。
上面的流程是给agent用来学习经验的。 每一场景都相当于一个培训课程。 在每个培训课程中, agent将探索环境 (由矩阵R表示), 接收奖励 (如果有), 直到达到目标状态。训练的目的是提高我们的agent的 “大脑”(矩阵 Q)。 场景越多,Q矩阵越优化。 在这种情况下, 如果矩阵 Q 得到了增强,四处探索时并不会在同一个房间进进出出, agent将找到最快的路线到达目标状态。
参数γ的范围为0到1(0 <= γ< 1)。 如果γ接近零,agent将倾向于只考虑立即得到奖励值。 如果γ更接近1,那么agent将会考虑更多的权重,愿意延迟得到奖励。
我们使用Python为训练agent编写代码:
import numpy as np
import random
# 初始化矩阵
Q = np.zeros((6, 6))
Q = np.matrix(Q)
# 回报矩阵R
R = np.matrix([[-1,-1,-1,-1,0,-1],[-1,-1,-1,0,-1,100],[-1,-1,-1,0,-1,-1],[-1,0,0,-1,0,-1],[0,-1,-1,0,-1,100],[-1,0,-1,-1,0,100]])
# 设立学习参数
γ = 0.8
# 训练
for i in range(2000):
# 对每一个训练,随机选择一种状态
state = random.randint(0, 5)
while True:
# 选择当前状态下的所有可能动作
r_pos_action = []
for action in range(6):
if R[state, action] >= 0:
r_pos_action.append(action)
next_state = r_pos_action[random.randint(0, len(r_pos_action) - 1)]
Q[state, next_state] = R[state, next_state] + γ *(Q[next_state]).max() #更新
state = next_state
# 状态4位最优库存状态
if state==5:
break
print(Q)
运行结果为:
这个矩阵Q可以通过将所有的非零条目除以最高的数字(在这种情况下为500)来归一化(即转换为百分比):
一旦矩阵Q足够接近收敛状态,我们知道我们的agent已经学习了任意状态到达目标状态的最佳路径。
例如:
从初始状态2开始,agent可以使用矩阵Q作为指导,从状态2开始,最大Q值表示选择进入状态3的动作。
从状态3开始,最大Q值表示有两种并列最优选择:进入状态1或4。假设我们任意选择去1。
从状态1开始,最大Q值表示选择进入状态5的动作。
因此,最优策略是2 – 3 – 1 – 5。
同时,若状态3时选择进入状态4,最优策略为2-3-4-5。
两种策略的累计回报值相等,故从状态2到5有两种最优策略。
# 例子较为简单,读者可以根据流程图和步骤解释手算以便加深印象。







 支付宝扫一扫
支付宝扫一扫 微信扫一扫
微信扫一扫





最新评论