高压油管的压力控制问题
摘 要：高压油管是许多燃油发动机的重要工作部件，而燃油进入和喷出高压油管会导致管内的压力发生变化，是影响燃油发动机工作效率的重要因素，因此，研究高压油管的压力控制问题对提高发动机工作效率具有重要意义。本文就高压油管工作过程中不同的进油和喷油方式建立了数学模型，研究了高压油管的压力控制问题。
对于问题一，首先分析密度和压力传播的变化特点，在高压环境下，将压力的非均匀变化问题简化为均匀变化问题，然后进行模型的建立与求解：第一步是用最小二乘法对附件3中弹性模量与压力的对应关系进行拟合，得出二次多项式关系；第二步是根据注1中给出的密度变化量和压力变化量的正比例关系计算出附件2中压力值对应的密度值，再次拟合得到密度与压力的关系式；第三步是通过进出高压油管的流量、单向阀和喷油嘴的工作时间等变量建立高压油管燃油量的变化模型；第四步是分析题目中要求高压油管内压力稳定在规定值的条件，由质量守恒定律得出密度随时间变化的模型，再结合压力与密度的关系模型建立高压油管内压力波动模型；第五步是确定第一小问模型，以总时间内压力波动最小为目标函数，以密度随时间变化的模型为约束条件，通过多次循环遍历的方法求得单向阀开启时长为0.2875ms时，高压油管内的压力能够维持在100MPa；第六步是在第一小问的模型的基础上加以修改，将总时间分别固定为2s、5s、10s时，同样通过多次循环遍历的方法得到当单向阀开启时长为0.7369ms时，高压油管内的压力可以从100MPa变为150MPa，并最终维持在150MPa左右；
对于问题二，考虑到高压油泵的凸轮通过拉动柱塞上下运动影响高压油管的进油流量，喷油嘴处的针阀上下运动影响高压油甘的出油流量。第一步，为求解高压油管的进油量，首先分析凸轮转动对高压油泵内压力和密度的影响，得出凸轮的不同角速度对应的油泵压力，然后分情况讨论高压油泵和高压油管内不同的压力大小关系对应的燃油流量，最后得出每一离散时刻点流入高压油管的燃油质量；第二步，为求解高压油管的出油量，首先求出针阀的升程对喷油面积的影响，通过分析针阀的结构，将针阀上升一定升程后与密封座之间形成的圆环面积和喷口面积中较小的一个作为喷油面积，然后根据注2中的流量模型确定燃油喷出时的流量，从而得出每一离散时刻点喷出高压油管的燃油质量；第三步，根据质量守恒定律得出高压油管内密度随时间变化的关系式，结合压力与密度的关系式，以总时间内压力波动最小为目标函数建立模型；第四步运用与问题一相似的求解方式，通过多次循环遍历的方法，不断调整参数，最终得出当凸轮角速度设置为0.02725
时，高压油管内的压力稳定在100MPa左右；
对于问题三，第一问是在问题二的基础上增加了一个喷油嘴，所以我们引入两个喷油嘴的开启时间差，分别确定两个喷油嘴对应的燃油流量以及每一个离散时刻点对应的流出的燃油的质量，修改问题二中质量守恒的关系式得到新的模型，求得此时凸轮的角速度与两个喷油嘴的开启时间差，作为调整高压油管的供油和出油策略的依据；第二问是在第一问的基础上增加了一个单向减压阀，所以需要考虑单向减压阀开启的压力临界值，同样修改模型中质量守恒关系式中的部分，得到新的模型，以此求出减压阀开启的压力临界值和此时凸轮的角速度分别作为减压阀和高压油泵的控制方案。
关键词：优化模型 离散模型 多重搜索 有限差分
1问题重述
燃油发动机工作的基础是燃油进入和喷出高压油管，燃油经过高压油泵进入高压油管，再由喷油嘴喷出。燃油进出高压油管这个间歇性工作过程会引起高压油管内部的压力的变化，从而使得喷出的燃油量出现不同程度的偏差，以此来影响发动机的工作效率，现需要通过控制单向阀开关的开启时间、凸轮的角度以及减压阀的开启条件等因素来控制高压油管内的压力变化。具体需要解决以下三个问题：
问题1.已知高压油管的内腔长度、内直径、供油入口小孔的直径、单向阀的工作规律、喷油器的工作规律和喷油速率等参数。当高压油泵入口提供的压力恒为160MPa时，要使高压油管内的压力稳定在100MPa，应该如何设置单向阀的单次开启时长？要使高压油管的压力经过2s、5s、10s的调整后稳定在150MPa，应该如何设置单向阀的单次开启时长？
问题2.实际工作过程中是通过控制高压油泵的凸轮来改变柱塞位置从而控制进入高压油泵的燃油量的，凸轮驱动柱塞上下运动，柱塞向上运动时压缩柱塞腔内的燃油，柱塞腔与高压油管之间通过单向阀连接，当腔内压力大于管内时单向阀开启，燃油进入高压油管内。柱塞运动到下止点时低压燃油充满柱塞腔（包括残余容积）。已知柱塞腔直径、柱塞运动到上止点时柱塞腔残余的容积、柱塞运动到下止点时低压燃油的压力、喷油嘴的针阀直径和密封座的结构等参数。在问题1中给出的喷油器工作次数、高压油管尺寸和初始压力下，当高压油管内的压力稳定在100MPa左右时，确定凸轮的角速度。
问题3.如果在问题2的基础上再增加一个同喷油规律的喷油嘴，应该如何调整喷油和供油的策略？为高压油管安装一个单向减压阀，给定减压阀的出口直径。打开单向减压阀可以使燃油在压力作用下回流到外部低压油路中从而减小高压油管内燃油的压力，在此种情况下给出高压油泵和减压阀的控制方案。
2问题分析
问题1：对于问题一，我们首先将压力的非均匀变化问题简化为均匀变化问题，然后进行模型的建立与求解。第一步是借助MATLAB软件，用最小二乘法对附件3中弹性模量与压力的对应关系进行拟合；第二步是根据注1中给出的密度变化量和压力变化量的正比例关系计算出附件2中压力值对应的密度值，再次拟合得到密度与压力的关系式；第三步是建立高压油管燃油量质量变化的模型；第四步是分析题目中要求高压油管内压力稳定在规定值的条件，由质量守恒定律得出密度随时间变化的模型，再结合压力与密度的关系模型建立高压油管内压力波动模型；第五步是确定第一小问模型；第六步是在第一小问模型的基础上加以修改，确定第二问的模型，在将总时间固定，同样通过多次循环遍历的方法分别观察单向阀开启时长的不同情况下的压力的波动情况，最终确定最优解；
问题2：对于问题二，考虑到高压油泵的凸轮通过拉动柱塞上下运动影响高压油管的进油流量，喷油嘴处的针阀上下运动影响高压油甘的出油流量。第一步，为求解高压油管的进油量，首先分析凸轮转动对高压油泵内压力和密度的影响，得出凸轮的不同角速度对应的油泵压力，然后分情况讨论进油口的燃油流量，最后得出每一离散时刻点流入高压油管的燃油质量；第二步，为求解高压油管的出油量，首先求出针阀的升程对喷油面积的影响，通过分析针阀的结构，确定喷油面积，然后根据注2中的流量模型确定燃油喷出时的流量，从而得出每一离散时刻点喷出高压油管的燃油质量；第三步，根据质量守恒定律得出高压油管内密度随时间变化的关系式，结合压力与密度的关系式，以总时间内压力波动最小为目标函数建立模型；
问题3：对于问题三，第一问是在问题二的基础上增加了一个喷油嘴，所以我们引入两个喷油嘴的开启时间差，分别确定两个喷油嘴对应的燃油流量以及每一个离散时刻点对应的流出的燃油的质量，修改问题二中质量守恒的关系式得到新的模型，确定调整高压油管的供油和出油的策略；第二问是在第一问的基础上增加了一个单向减压阀，所以需要考虑单向减压阀开启的压力临界值，同样修改模型中质量守恒关系式中的部分，得到新的模型，以此确定减压阀和高压油泵的控制方案。
3模型假设与符号说明
3.1模型假设
①假设高压油管中的气体分子是均匀分布的，在各处的压强和密度是相等的；
②假设高压油管是理想圆柱体，忽略进油口和出油口对管内分子分布的影响；
③假设研究过程中整个系统的温度变化可以忽略；
④假设单向阀开关和单向减压阀的操作时间足够短，可以忽略不计；
⑤假设进油和出油过程中燃油对管内压强产生改变的时间足够短，可以不考虑液体压力波动和压力传播时间；
⑥假设进油口和出油口的位置对管道压强的影响可以忽略不计。
3.2符号说明
表1 符号说明表
|
符号 |
含义 |
单位 |
|
|
表示弹性模量 |
|
|
|
表示每一个离散时刻点高压油管内对应的压力值 |
|
|
|
表示高压油管内的起始压力值 |
|
|
|
表示研究总时间的长度 |
|
|
|
由附件2中针阀运动曲线的时间间隔得到，设定为离散点的步长 |
|
|
|
|
|
|
|
|
|
|
|
表示一个进油周期内每一时间段流进高压油管内油的质量 |
|
|
|
表示一个出油周期内每一时间段流出高压油管外油的质量 |
|
|
|
表示高压油泵在进口处提供的压力对应的密度值 |
|
|
|
表示高压油管中每一时刻的压力值对应的密度值 |
|
|
|
表示高压油管中初始的密度值 |
|
|
|
表示一个进油周期内流入高压油管内油的体积 |
|
|
|
表示一个出油周期内流出高压油管外油的体积 |
|
|
|
表示喷油嘴的喷油速率 |
|
|
|
表示所研究的时间段内任意一个时刻点对应的时间 |
|
|
|
表示高压油管的内腔长度，值为500mm |
|
|
|
表示高压油管的内直径，值为10mm |
|
|
|
表示高压油泵中每一时刻对应的密度 |
|
|
|
表示高压油管进油口的小孔直径，值为1.4mm |
|
|
|
表示初始状态时凸轮转轴到最远边缘点的极径 |
|
|
|
表示高压油泵的横截面积 |
|
|
|
表示进油口的流量在每一时刻的值 |
|
|
|
表示出油口的流量在每一时刻的值 |
|
|
|
表示单向减压阀开启的压力临界值 |
|
4模型准备
4.1压力和密度关系式的确定
由注1可知燃油压力的变化量与密度的变化量成正比，即：
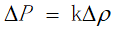（1）
且比例系数k：
（2）
附件3给出401组弹性模量与压力的对应数据，我们需要根据这些数据得出二者的函数关系.通过初步分析确定待定函数是线性，为建立这样一个模型，通常采用线性拟合的方法，通过比较拟合优度与1的接近程度来确定所得函数关系式是否可以代表数据之间的关系。我们在MATLAB中用polyfit进行拟合：
图1 弹性模量与压力关系式拟合图
得到拟合优度为0.9991的回归方程，表示弹性模量与压力的关系式为：
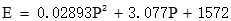（3）
通过上述关系式得到压力变化量与密度变化量的关系为：
（4）
将附件3中压力的数据代入（4）式计算出对应的密度的值（附件1），再次在MATLAB中用polyfit进行拟合：
图2 压力与密度关系式拟合图
得到拟合优度为1的回归方程，表示压力与密度的关系式为：
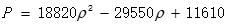（5）
4.2极径与极角关系式的确定
由附件1中给定的凸轮边缘曲线中极径和极角的数据进行线性拟合，绘制极径与极角的变化关系图，得到拟合曲线如图3所示：
图3 极径与极角关系拟合曲线图
得到极径与极角之间的关系式为：
（6）
5模型的建立与求解
5.1问题一模型的建立与求解
5.1.1模型的建立
模型一：高压油管内燃油质量变化模型
问题一要求设置单向阀的单次开启时长以控制高压油管内因进油和出油过程中高压油管内的压强尽可能稳定，即每一时刻的压强与初始压强的偏差值的总和最小，我们以离散点的方式求压强偏差值的总和，并以此为目标函数建立如下目标优化模型：
（7）
为保证研究时间段内包括进油和出油的所有对应情况，我们选取总时间T为一个进油周期与一个出油周期的乘积。
（8）
对于进油过程：
①设一个进油周期的总时长为
（9）
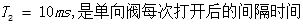
②设一个进油周期内进入高压油管的油的体积为
（10）
③得到一个进油周期内进入高压油管的油的质量为
（11）
对于出油过程：
①设一个出油周期的总时长为
（12）
由题目中给出的喷油速率与时间的关系图
图4 喷油速率与时间关系图
得出喷油速度为
（13）
所以
（14）
③得到一个出油周期内流出高压油管的油的质量为
（15）
模型二：高压油管内压力波动模型
对于总体来说
（16）
为保证高压油管工作过程中，管内压力维持在稳定状态，即保证每一时刻进出油的质量相同,由于高压油管的体积不变，由质量守恒定律可得：
（17）
由此得到
（18）
综上所述，问题一的模型为：
5.1.2模型的求解
对于设置单向阀开启时长将高压油管内的压力稳定在100MPa的要求，我们的求解步骤如下：
①首先设置初始时刻为0，此时单向阀与喷油嘴同时开始工作，且认为二者的工作方式均为先打开，再关闭，如此周期性循环进行。
②接下来开始进行寻优解的过程，设置单向阀的开启时长范围为0.1~10ms，设置步长0.05ms计算高压油管在每一时刻点对应的压力如图1所示：
图5 时间-压力变化图(0.1~10ms)
由图可以得到，当高压油管内压力为100MPa时，单向阀的开启时间在0.25ms左右，据此进一步确定单向阀的开启时长；
③设置单向阀的开启时长为0.25ms~0.29ms，缩小步长至0.01ms，同样计算每一时间点对应的高压油管的压力值，得到如图5所示的结果：
图6 时间-压力变化图(0.25ms~0.29ms)
④再次设置单向阀的开启时长为0.285ms~0.290ms，缩小步长至0.001ms，得到如图6所示的结果：
图7 时间-压力变化图(0.285ms~0.290ms)
从图中标记的坐标点可以看出单向阀开启时长的最优解在0.287ms~0.288ms的范围内，我们再次进行了范围的精确化，得到图7所示的结果：
图8 时间-压力关系图
当单向阀的开启时长设定为0.2875ms的时候，高压油管内的压力值为99.9919MPa，非常接近题目要求的100MPa。
⑤当设置单向阀的开启时长为0.2875ms时，我们得到高压油管内的压力变化程度如图8所示：
图9 压力变化程度
从图中可以看出此时高压油管内的压力基本上维持在100MPa左右，且波动幅度不大，所以我们取解为：
对于设置单向阀开启时长使高压油管的压力分别经过2s、5s、10s的调整后稳定在150MPa的要求，我们的求解步骤如下：
①通过最小二乘法进行拟合，如图9所示，得出高压油管内的压力达到150MPa需要的进油时间，即单向阀开启的时长为0.7369ms；
图10 高压油管压力达到150MPa对应的进油时间
②由题目要求，工作总时间分别为2s、5s、10s，借助MATLAB软件对压力和时间的关系进行拟合作图：
图11 调整时间为2s时高压油管内压力随时间变化规律
当调整时间为2s=2000ms时，单向阀的开启时间为：
Time=-0.0001*gap+0.9369; gap<2000;
Time=0.7369; gap>=2000;
图12 调整时间为5s时高压油管内压力随时间变化规律
当调整时间为5s=5000ms时，单向阀的开启时间为：
Time=0.0001*gap+0.2369; gap<5000;
Time=0.7369; gap>=5000;
图13 调整时间为10s时高压油管内压力随时间变化规律
当调整时间为10s=10000ms时，单向阀的开启时间为：
Time=0.00004*gap+0.3369;gap<10000
Time=0.7369; gap>=10000
综上所述：
①要使高压油管内的压力稳定在100MPa，应该设置单向阀的单次开启时长为0.2875ms；
②要使高压油管的压力经过2s、5s、10s的调整后稳定在150MPa，应该设置单向阀的单次开启时长为0.7369ms
5.2问题二模型的建立与求解
5.2.1模型的建立
问题二给定高压油管进油口高压油泵的工作原理和出油口喷油嘴的工作原理，沿用问题一中的目标函数：
（19）
对于约束条件，首先分析不同工作原理下进油和出油的方式：
①对于进油口的高压油泵：
图14 凸轮工作原理分析图
如图13所示，以凸轮转轴为原点建立二维坐标系，设定凸轮转动方向是逆时针方向，以图中实线凸轮的位置作为凸轮的初始位置，此时凸轮边缘线最高点为A(x,y)，当凸轮转动一定角度到达虚线凸轮位置时，会拉动高压油泵中的柱塞上下运动，从而改变高压油泵的内部压力。转动后凸轮边缘线最高点为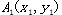
。
（20）
当凸轮以角速度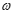
转动t时间，凸轮的边缘线最高点的纵坐标为
（21）
所以凸轮转动拉动柱塞上下运动引起的高压油泵内体积变为
（22）
假定高压油泵中燃油的总质量是不变的，即有燃油流入高压油管的同时，会有燃油补充进高压油泵的柱塞腔。由题目信息得知当柱塞位于下止点时高压油泵内的压力值，根据压力与密度的关系式可以得到此时对应的密度值，所以高压油泵中燃油的质量为
（23）
由密度公式，可根据每一个离散时刻点对应的油泵体积计算每一个离散时刻点油泵内的密度：
（24）
根据密度与压力的关系式，可得到每一个离散时刻点高压油泵内的压力为：
（25）
②对于进油口的进油过程：
由于高压油泵的进油原理是柱塞向上运动增大高压油泵内的压力，当高压油泵里的压力大于高压油管中的压力时，连接二者的单向阀才会开启，进油口才会有油流入，根据注2中流量模型，本问中高压油管进油口的流量为：
（26）
注：其中C=0.85为流量系数，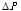
为小孔两侧的压力差(MPa)，
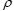为高压侧燃油的密度(
)
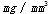根据以上模型推导得到进油质量模型为
（27）
③对于出油口的喷油嘴：
图15 喷油嘴工作原理分析图
由题意得，针阀直径为
，喷孔直径为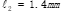
；
设针阀关闭时距离喷孔密封座顶角的距离为h，针阀的升程为h(t)，则可得到针阀上升后针阀底部同一平面内与密封座边缘形成的圆环的面积为：
（28）
考虑到燃油顺利流出，避免堵在喷油嘴的密封座中，对于喷孔喷出燃油的横截面积，应该取圆环面积和喷口面积中较小的一个：
（29）
④对于出油口的喷油过程：
结合注2中给出的燃油流量模型，得出燃油流出高压油管时的流量为：
（30）
由此得到高压油管中流出的燃油的质量模型为：
（31）
对于总体来说，根据质量守恒定律可得
（32）
综上所述，问题二的模型为
5.2.2模型的求解
问题二的模型基本上与第一问相同，只是改变了进油量和出油量的计算方法，所以求解也类似与问题一的求解过程：
①首先设置凸轮角速度的范围，通过多次调整参数，循环逼近求解，最终将角速度范围确定在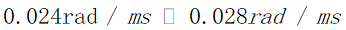
，设置求解步长为0.0001
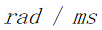，可以近似将最优解确定在0.02725
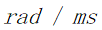，得到压力与角速度之间的关系曲线图如下：
图16 高压油管内压力与凸轮角速度关系图
在角速度取最优解的值时，对应压力随时间变化的图像如下：
图17 压力与时间关系图
由图像可以看出，在凸轮角速度设置为0.02725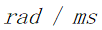
时，随着工作时间的变化，高压油管内的压力稳定在100MPa附近，符合题设要求。
5.3问题三模型的建立与求解
5.3.1模型的建立
①第一问
首先分析问题三的第一问是在问题二的基础上增加了一个喷油嘴，同样考虑进油量和出油量。
以最终压强偏差值的总和，为目标函数建立如下目标优化模型：
（33）
对于进油口的进油过程：
沿用问题二中的进油量模型
（34）
对于出油口的喷油过程：
增加一个喷油嘴之后，其工作规律与第一个喷油嘴是相同的，在高压油泵的工作规律不发生改变的情况下，我们需要考虑两个喷油嘴开启时间之间的时间差，在此种情况下得到高压油泵的转轮的角速度。
对于喷油嘴1和喷油嘴2的流量，我们考虑从发动机工作起始时间点开始，喷油嘴之间开启时间差设置为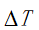
，则两个喷油嘴喷油时的流量为：
（35）
（36）
两个喷油嘴喷喷出的油的质量为
（37）
（38）
由质量守恒定律得到
（39）
②第二问
为高压油管添加减压阀之后，设计高压油泵和减压阀的控制方案，即解决高压油泵中凸轮的角速度与减压阀开启时间的对应方案。
以第一问中求解得出的作为第二问中两个喷油嘴的开启时间差，由质量守恒定律得到此时
（40）
设置当高压油管内的压力大于一个值的时候，单向减压阀开启，由注2中的流量模型修改得到通过减压阀的燃油的流量为
（41）
则通过减压阀流出的燃油的质量为
（42）
综上所述：
本题第一问需要根据模型求解凸轮角速度以及两个喷油嘴的开启时间差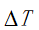
。
本题第二问需要在第一问中喷油嘴开启时间差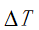
确定后，根据模型求解此时凸轮角速度以及减压阀开启的压力临界值。
5.3.2模型的求解
①第一问
针对喷油和供油策略，分别调整两个喷油嘴开启时间之间的间隔和凸轮的运动角速度，由于参数之间相互影响，所以我们将不同参数调整共同进行。
利用多重搜索的方式搜索两个喷油嘴的开启时间间隔，在每一间隔数值下调整凸轮运动角速度，使得高压油管内的压力稳定在100MPa。当喷油嘴开始喷射时间间隔在0-50ms变化时，压力在时间间隔12.5ms、37.5ms、50ms时变化如图18-20所示。
|
图18 时间间隔为12.5ms时压力
|
|
图19 时间间隔为37.5ms时压力
|
|
图20 时间间隔为50ms时压力
|
分析上图可以得到，在0-50ms时间间隔内，管内压力波动幅度减小；
当时间间隔在0-100ms之间变化时，压力差的变化曲线如下图：
图21 压力变化曲线
由图可以看出，延迟时间在50ms附近时，压力差最小，在此点附近进行精确搜索，得到最优时间间隔差为
。
②第二问
引入单向减压阀后，调整喷油策略和供油策略，当高压油管内压力大于临界值时，单向阀开启，搜寻临界值压力与凸轮旋转角速度。
当波动误差为:0.101MPa，喷油角速度为0.126rad/ms，喷油周期为50.000ms时，阀流速和压力差之间的关系如图：
图22 阀流速与压力差变化关系图
此时压力与时间的关系如下图：
图23 压力与时间关系图
最终解得：
6模型总结
模型的建立有以下优点：
①整篇文章的模型以第一问的模型为基础层层递进，模型推广性良好；
②采用多重搜索算法，提高求解速度，且算法得可重复利用性强。
同时模型的建立也具有一些缺点：
①模型的建立过程中将压力的不均匀变化简化成了均匀变化，在实际情况中模型的结果会有一定的偏差；
②高压油泵中得具体运动没有仔细考虑，过于理想化。
参考文献
[1].王想义，张磊，张若凌，蒋劲．燃烧室高温燃油的密度变化特性及控制方法研究[J/OL]．实验流体力学
[2].叶涵沈陆娟赵沈杰柯玉荷 《基于全局优化模型高压油管压力控制研究》[J].科学技术创新 2021.16
[3].宋常修张善莹崔忠瑞张雅婷邵玉昕 《高压油管的压力控制方案》[J]. 工业技术创新第08卷第02期 2021年4月
[5].余婷陈志宏田晨晨金树林冯继林 《高压油管的压力控制》[J].内江科技 2021年第三期
[6].邹萌，刘仲望，邓攀羽《单向阀对高压油管压力的动态控制》[J]. 装备与自动化 2020 年第 6 期
[7].许元振房义孙思荣朱婧《基于多重搜索算法的高压油管压力控制策略》[J]. 数学建模及其应用 第9卷第4期 2020年12月
附录：本次程序文件单独打包
结语：这次练习代码难度有些大，有许多借鉴优秀论文中的代码，不是我说，代码真滴难写，无数种迭代，代码调试就调试了2天，最后好像还错了，hhh，不过幸亏稍微调整了下参数变量，让图看起来没有什么太大的问题。不过最终结果是好的，在最后一天成功提交了。去实验室感觉自己人都吃胖了，各种零食，糖，牛肉干，这就是实验室版食堂嘛。对了，要是那天血糖突然高了，肯定是黄sir天天拿一堆糖的原因。这里也可怜一下纪某人的腿hhhh
代码：Modeling/高压管/代码 at master · instead-everyone/Modeling (github.com)
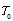
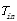
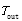
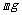
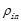
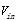
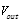
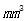
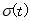
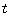
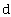
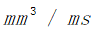
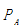
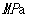
支付宝扫一扫
微信扫一扫
最新评论