本篇文章第一部分翻译自：http://www.wildml.com/2015/10/recurrent-neural-networks-tutorial-part-3-backpropagation-through-time-and-vanishing-gradients/，英文好的朋友可以直接看原文。

最近看到RNN，先是困惑于怎样实现隐藏层的互联，搞明白之后又不太明白如何使用BPTT进行训练，在网上找资源发现本篇博客介绍较为详细易懂，自己翻译了一遍，以下：

RNN教程，第3部分，通过时间反向传播（BPTT）和梯度消失

这是RNN教程的第三部分。

在本教程的前面部分我们从头开始实现了一个RNN网络，但是没有探究实现BPTT计算梯度的细节。在这部分我们将给出BPTT的简要概述并且解释它和传统反向传播算法的区别。随后我们将致力于理解梯度消失问题（vanishing gradient problem），这个问题促成了LSTMs和GRUs的发展，在NLP（和其他领域），它们是当前最受欢迎和最为强大的模型中的两种。梯度消失问题最早于1991年有Sepp Hochreiter发现，最近由于深度结构的应用增多而重新受到关注。

如果想完全理解这部分内容，我建议你对偏导数和基本的反向传播工作很熟悉。如果你还不熟悉，你可以从【文中提供了三个地址】找到好的教程，它们随着难度的上升而排序。

Backpropagation Through TIme（BPTT）

我们先快速回顾一下RNN的等式。注意到这里有一个小变化，符号o变成了RNN训练算法BPTT介绍-风君雪科技博客RNN训练算法BPTT介绍-风君雪科技博客。这是为了和我参考的一些文献保持一致。

RNN训练算法BPTT介绍RNN训练算法BPTT介绍

我们同时定义我们的损失函数（或者称为误差）为交叉熵损失，由以下公式给出：

RNN训练算法BPTT介绍RNN训练算法BPTT介绍

这里RNN训练算法BPTT介绍-风君雪科技博客RNN训练算法BPTT介绍-风君雪科技博客是t时刻的正确单词，RNN训练算法BPTT介绍-风君雪科技博客RNN训练算法BPTT介绍-风君雪科技博客是网络的预测。典型的，我们将完整的序列（句子）是为一个训练实例，所以总的误差是各个时间点（单词）误差的和。

RNN训练算法BPTT介绍RNN训练算法BPTT介绍

我们的目的是计算误差关于参数U，V和W的梯度并通过随机梯度下降（SGD）来学习好的参数。正如我们计算了误差的和，我们也将一个训练实例各个时间地啊你的梯度做一个求和：\frac{\partial E}{\partial W} = \sum\limits_{t} \frac{\partial E_t}{\partial W}\frac{\partial E}{\partial W} = \sum\limits_{t} \frac{\partial E_t}{\partial W} 。

我们使用链式求导来计算这些导数。这是从误差开始后应用反向传播算法。在这篇文章的剩余部分我们将使用 E_3E_3作为例子，这只是为了用一个实际的数来做推导。

\begin{aligned} \frac{\partial E_3}{\partial V} &=\frac{\partial E_3}{\partial \hat{y}_3}\frac{\partial\hat{y}_3}{\partial V}\\ &=\frac{\partial E_3}{\partial \hat{y}_3}\frac{\partial\hat{y}_3}{\partial z_3}\frac{\partial z_3}{\partial V}\\ &=(\hat{y}_3 - y_3) \otimes s_3 \\ \end{aligned}\begin{aligned} \frac{\partial E_3}{\partial V} &=\frac{\partial E_3}{\partial \hat{y}_3}\frac{\partial\hat{y}_3}{\partial V}\\ &=\frac{\partial E_3}{\partial \hat{y}_3}\frac{\partial\hat{y}_3}{\partial z_3}\frac{\partial z_3}{\partial V}\\ &=(\hat{y}_3 - y_3) \otimes s_3 \\ \end{aligned}

在上面的式子中，z_3 =Vs_3z_3 =Vs_3，同时\otimes\otimes表示两个向量的外积运算。如果上面讲的你跟不上也不用担心，我跳过了一些步骤，你可以自己尝试计算这些导数（这是一个很好的锻炼！）。我想从上面式子中得到的是\frac{\partial E_3}{\partial V}\frac{\partial E_3}{\partial V}的计算仅仅依赖于当前时间点的数值\hat{y}_3, y_3, s_3\hat{y}_3, y_3, s_3。如果你掌握着这些，计算误差关于V的导数就仅仅是一个简单的矩阵乘法。

但是对于\frac{\partial E_3}{\partial W}\frac{\partial E_3}{\partial W}（和U）的情况却是不同的。我们列出链式法则来一探究竟，与上面类似：

\begin{aligned} \frac{\partial E_3}{\partial W} &= \frac{\partial E_3}{\partial \hat{y}_3}\frac{\partial\hat{y}_3}{\partial s_3}\frac{\partial s_3}{\partial W}\\ \end{aligned}\begin{aligned} \frac{\partial E_3}{\partial W} &= \frac{\partial E_3}{\partial \hat{y}_3}\frac{\partial\hat{y}_3}{\partial s_3}\frac{\partial s_3}{\partial W}\\ \end{aligned}

现在应该注意到的是s_3 = \tanh(Ux_t + Ws_2)s_3 = \tanh(Ux_t + Ws_2)依赖于s_2s_2，而s_2s_2又依赖于W和s_1s_1，以此类推。如果我们计算关于W的导数我们不能简单地将s_2s_2视为常量！我们需要再次使用链式法则，我们最终获得的表达式为:

\begin{aligned} \frac{\partial E_3}{\partial W} &= \sum\limits_{k=0}^{3} \frac{\partial E_3}{\partial \hat{y}_3}\frac{\partial\hat{y}_3}{\partial s_3}\frac{\partial s_3}{\partial s_k}\frac{\partial s_k}{\partial W}\\ \end{aligned}\begin{aligned} \frac{\partial E_3}{\partial W} &= \sum\limits_{k=0}^{3} \frac{\partial E_3}{\partial \hat{y}_3}\frac{\partial\hat{y}_3}{\partial s_3}\frac{\partial s_3}{\partial s_k}\frac{\partial s_k}{\partial W}\\ \end{aligned}

我们将每个时间点对梯度的贡献求和。话句话说，由于在到达我们所关心的输出的过程中的每一步计算中都用了W，我们需要从t=3开始在网络中的每一个路径反向传播梯度直到t=0。

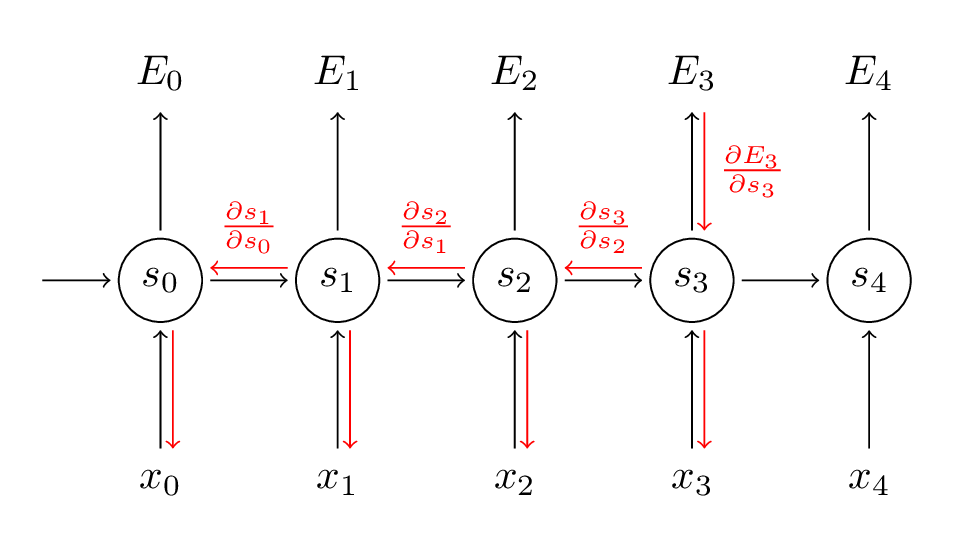
RNN训练算法BPTT介绍RNN训练算法BPTT介绍

注意到这和我们在深度前向神经网络中使用的标准反向传播算法是一样的。最主要的区别在于我们计算了关于W每个时间点上的梯度并将它们求和。传统神经网络中我们不会在层间分享参数，所以也不用做任何求和。但是在我看来BPTT不过是标准反向传播在没展开的RNN的一个有趣的名字。类似反向传播你可以定义一个向后传播的δ矢量，例如：\delta_2^{(3)} = \frac{\partial E_3}{\partial z_2} =\frac{\partial E_3}{\partial s_3}\frac{\partial s_3}{\partial s_2}\frac{\partial s_2}{\partial z_2}\delta_2^{(3)} = \frac{\partial E_3}{\partial z_2} =\frac{\partial E_3}{\partial s_3}\frac{\partial s_3}{\partial s_2}\frac{\partial s_2}{\partial z_2}，这里z_2 = Ux_2+ Ws_1z_2 = Ux_2+ Ws_1。然后应用相同的方程式。

一个简单的BPTT实现类似于下面的代码：

RNN训练算法BPTT介绍RNN训练算法BPTT介绍

翻译结束,原文后续部分探讨梯度消失。

推到一下上面的公式：

RNN训练算法BPTT介绍RNN训练算法BPTT介绍

部分参考;

http://blog.sina.cn/dpool/blog/s/blog_6e32babb0102y3u7.html