
欢迎大家关注我们的网站和系列教程:http://www.tensorflownews.com/ ,学习更多的机器学习、深度学习的知识!
荔枝boy
卷积神经网络的发展
卷积神经网络的重要性
卷积神经网络与图像识别
滤波器
一.卷积神经网络的发展
卷积神经网络受到视觉细胞研究的启发,1962年,Hubel和Wiesel发现初级视觉皮层中的神经元会响应视觉环境中特定的简单特征(比如有向的边等)。同时,他们注意到了两种不同类型的细胞,简单细胞和复杂细胞,简单细胞只对非常特定的空间位置,对它们非常偏好的方向有强烈的反应,复杂细胞有更大的空间不变性,复杂细胞通过几个简单细胞(每个简单细胞存在不同方向的偏好)的输入上进行池化而实现这种不变性。这两个特征即对特定特征的选择和通过前馈连接增大空间不变性构成了卷积神经网络的人工视觉基础。
计算机视觉领域中有一个比赛叫做ImageNet挑战赛,相当于计算机视觉的年度诺贝尔。2012年,Alex Krizhevsky凭借卷积神经网络获得那一年的冠军,他把图片分类误差从原来的26%降低到15%,这在计算机视觉领域引起了不小的轰动。并让卷积神经网络在如今计算机视觉领域中占据着很重要的一部分。
二.卷积神经网络的重要性
1.局部连接
在第三章中,我们介绍前馈神经网络的时候,相邻的两层之间,前一层的每一个神经元(或输入层的每一个单元)与后一层的每一个神经元都有连接,这种情况称为全连接。全连接网络的一个缺点就是参数太多,假设我们输入到神经网络中的是一张三通道的彩色图像,图像大小为128128,因此输入层有128128*3=49150个单元。使用全连接网络的话,第一个隐藏层的每一个神经元到输入层都有49150个连接,随着网络层数的增加和每层中神经元数量的增加,网络中的参数也会急剧增加。大量的参数不仅会拉低神经网络训练的效率,也很容易导致过拟合。
在卷积神经网络中,层与层之间不再是全连接,而是局部连接,具体的实现方法,就是我们在下一节中会介绍的卷积操作。
卷积神经网络属于局部连接网络,是基于深刻研究自然图像而提出来的。自然图像存在局部区域稳定的属性,其某一局部区域的统计特征相对于图像其他相邻局部区域具有相似性。因此,神经网络从自然图像中学习到的某一局部区域特征同样适合于图像的其他相邻局部区域。
2.权值共享
卷积神经网络中的卷积层中会有很多的滤波器,这些滤波器会去识别图像的特定的某些特征,每个滤波器会去滑动卷积上一层的特征图,在卷积的过程中滤波器的参数是不变且共享的。这样在训练过程中,与之前的全连接神经网络训练大尺度输入样本时需要大量参数相比,卷积神经网络只需要很少的参数就可以完成训练。(CNN图像的平移不变性)
3.子采样
子采样层(subsampling layer)也叫作汇聚层(pooling layer), 对上一卷积层层进行聚合,使得上一层卷积层的输入特征图尺寸在经过该子采样层的聚合也就是我们说的池化后减小了。子采样层所做的事其实就是对上一层卷积层进行扫描,每次扫描特定区域,然后一般计算该区域特征的最大值或者平均值,放入子采样层的窗口中。
三.卷积神经网络与图像识别
计算机视觉领域中很多的问题是处理图像识别即图像分类。图像分类是对于输入的图像进行操作后,最终输出一组描述图像分类的概率。当计算机看到一张图片时,在它的理解中,这张图片是一个大小MN3的像素矩阵(3指的是RGB的值),其中像素矩阵中每个像素的值在0到255之间。对于计算机来说,在给定计算机这个像素矩阵作为输入后,计算机要输出能够描述出该图像属于各种类别的概率(eg:[狗:80%,猫10%,兔子10%])
当人分析了一幅图像时,首先会看这个物体有哪些局部的特征,比如如果图片是一条狗,我们在看这幅图像时,在看到诸如鼻子或四条腿等明显特征后,我们会把它归类为狗。卷积神经网络和人的视觉细胞工作原理类似,卷积神经网络也是一开始通过寻找这副图片的边缘或者曲线等低级特征来分类图片,然后再通过一系列卷积层将这些低级的特征汇聚成更加高级的特征,同时这些高级的特征由多个低级特征卷积构成,则高级特征能覆盖原始图片更多的信息。这样卷积神经网络在处理一些经过平移变换的图像识别时,具有检测平移不变性的能力。更加增强了卷积神经网络在图像识别的能力。
四.滤波器
在讲解CNN之前,我们先讨论下滤波器。
滤波器是一个矩阵,大小为m*n它是用来检测图像中特定的特征的,不同的滤波器有不同的参数。
我们知道图像在计算机中的数字信号其实是MN3大小的矩阵,假设我们只考虑图像的灰度,不考虑RGB,那么图像的大小为MN。某一个滤波器对图像进行滤波时,就是将滤波器分别与图像的同大小区域进行点乘,每次滤波器依次从左往右从上往下滑过该图像所有的区域,让该滤波器对图像的某一个与滤波器尺寸同大小的图像区域(mn)进行点乘,点乘后各个乘积求和得到新的过滤后的图像,这种图像某一部分与滤波器点乘后求和操作就是以后的卷积神经网络中的卷积操作,这样就得到了经过滤波器过滤后的图像。
不同的滤波器可以检测图像的不同特征,举个例子,假设现在我有一个滤波器用来检测特定弧度,大小为7*7。
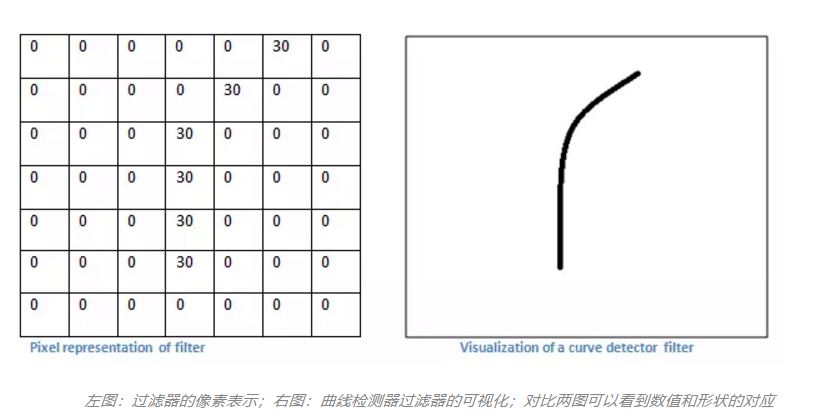
现在我有一个老鼠的图像(只考虑灰度,所以只有一层),现在我们用该滤波器对这只老鼠的图像进行过滤,依次将过滤器滑过原始图像的某一个区域,并与该区域原始像素值进行点乘。现在假设我们将滤波器滑到了老鼠图像的左上角,如图二所示:
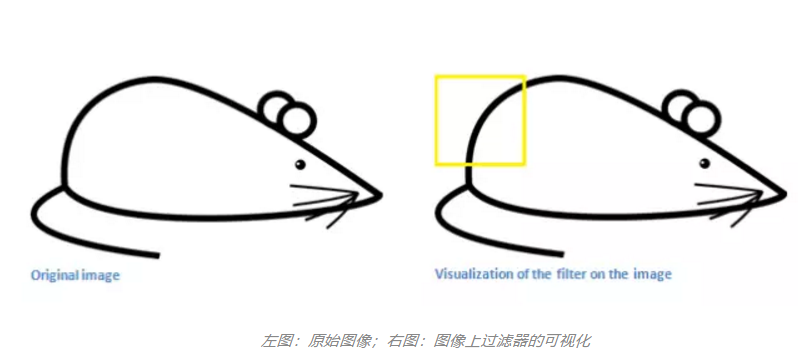
过滤器会与该原始图像对应区域进行点乘后求和,如图三所示:
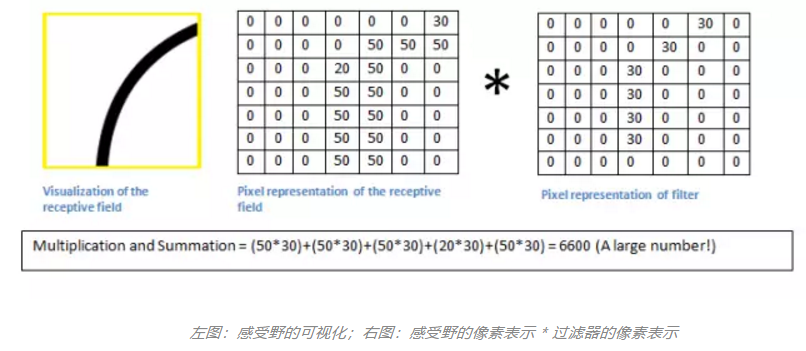
我们发现,该区域本身存在一个弧度,且弯曲程度和过滤器的弯曲程度很相似,所以图像的该区域像素与过滤器矩阵点乘求和后得到的数值很高。
我们继续将过滤器移动到另外一个地方,靠近老鼠耳朵的地方,这时候我们发现该老鼠耳朵区域与该滤波器用来检测的弧度很不相似,我们看看将用滤波器过滤该区域会发生什么,如图四所示:
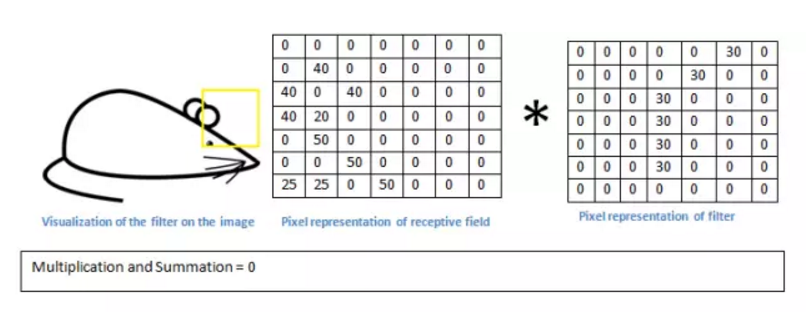
我们发现,检测弧度的滤波器再与老鼠耳朵这个区域的像素进行点乘后求和所得到的值为0。也就是说该区域与滤波器没有对应关系。
我们对整个原图进行一次卷积,得到的结果中,在那个特定曲线和周边区域,值就很高,在其他区域,值相对低。这就是一张激活图。对应的高值区域就是我们所要检测曲线的位置
所以我们发现滤波器过滤图像时,会与图像每个等大的区域进行点乘,如果图像的某一区域与过滤器检测的特征很相似,那么当过滤器经过该区域时,就会激活该过滤器,得到一个很高的值,反之,如果图像的某一区域与过滤器检测的特征很不相似时,就不会激活该过滤器或者得到的数值很低。
由此我们发现,图像的过滤器在对整个图像滑动过滤时,每经过图像一个区域得到的值越高,则该区域与滤波器检测的特定特征相关度越高。这里与视觉细胞的工作原理很类似,简单的细胞对特定方向具有强烈感应,对不是它们偏好的方向没有什么反应。这里的滤波器其实就充当了视觉细胞中简单细胞的角色。
一些检测特定特征的滤波器很容易想到,比如水平滤波器,垂直滤波器等。
但是我们能直观想到滤波器毕竟数量有限,而CNN可以自动学习滤波器,调整滤波器里的参数,用CNN自学习滤波器,让计算机自己去理解这图像所需的滤波器来检测特征,这对图像的特征分析是非常有用高效的。

 支付宝扫一扫
支付宝扫一扫 微信扫一扫
微信扫一扫










最新评论