
我们设一个圆的圆心坐标为 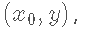 ,半径为 r 。那么这个圆的方程可以写为:
,半径为 r 。那么这个圆的方程可以写为: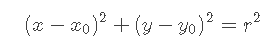
在这个圆上随便取三个点,设这三个点的坐标分别是 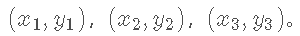 那么有:
那么有:
公式(1)(2)相减,(1)(3)相减之后经过化简可以得到:
简单变变型也就是: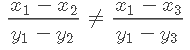
这样写几何含义就很明显了,三点不能共线。
有了 x 0 和 y 0 的值后,带入(1) 式就可以得到 r 的值。至此,三点确定圆的问题就解决了。
三点共圆求圆心的模版:
double X, Y; struct Point { double x, y; } a[2005]; void solve(Point a, Point b, Point c) //三点共圆圆心公式 { double fm1=2 * (a.y - c.y) * (a.x - b.x) - 2 * (a.y - b.y) * (a.x - c.x); // 2 (da - bc) double fm2=2 * (a.y - b.y) * (a.x - c.x) - 2 * (a.y - c.y) * (a.x - b.x); // 2 (bc - ad) if (fm1 == 0 || fm2 == 0) { X = Y = 1e18; return; } double fz1=a.x * a.x - b.x * b.x + a.y * a.y - b.y * b.y; // e double fz2=a.x * a.x - c.x * c.x + a.y * a.y - c.y * c.y; // f X = (fz1 * (a.y - c.y) - fz2 * (a.y - b.y)) / fm1; // x0 Y = (fz1 * (a.x - c.x) - fz2 * (a.x - b.x)) / fm2; // y0 }
例题:Boundary
题意:
给了n个点,让你自己随便定义圆心(圆心不要求是n个点的其中一个)和半径,要求这n个点有尽可能多的点在圆上,并且该圆经过坐标原点(0,0)。求满足的圆上的点最多有多少个。
想法:
由于必须经过原点,所以我们可以只枚举两个点从而就可以达到枚举圆心的目的。【因为三点共圆】
用vector保存下来这些圆心坐标。
处理完后,对圆心坐标sort一下,判断有多少个圆心坐标是一样的。
再要寻找有几个点在圆上,我们可以枚举圆上的点。
满足 x * (x – 1 ) / 2 == ans
这个时候的 x 就是我们所求的
#include <algorithm> #include <string> #include <cstring> #include <vector> #include <map> #include <stack> #include <set> #include <queue> #include <cmath> #include <cstdio> #include <iomanip> #include <ctime> #include <bitset> #include <cmath> #include <sstream> #include <iostream> #include <unordered_map> #define ll long long #define ull unsigned long long #define ls nod<<1 #define rs (nod<<1)+1 #define pii pair<int,int> #define mp make_pair #define pb push_back #define INF 0x3f3f3f3f #define max(a, b) (a>b?a:b) #define min(a, b) (a<b?a:b) const double eps = 1e-8; const int maxn = 2e5 + 10; const ll MOD = 99999999999999; const int mlog=20; int sgn(double a) { return a < -eps ? -1 : a < eps ? 0 : 1; } using namespace std; double X, Y; struct Point { double x, y; } a[2005]; void solve(Point a, Point b, Point c) //三点共圆圆心公式 { double fm1=2 * (a.y - c.y) * (a.x - b.x) - 2 * (a.y - b.y) * (a.x - c.x); // 2 (da - bc) double fm2=2 * (a.y - b.y) * (a.x - c.x) - 2 * (a.y - c.y) * (a.x - b.x); // 2 (bc - ad) if (fm1 == 0 || fm2 == 0) { X = Y = 1e18; return; } double fz1=a.x * a.x - b.x * b.x + a.y * a.y - b.y * b.y; // e double fz2=a.x * a.x - c.x * c.x + a.y * a.y - c.y * c.y; // f X = (fz1 * (a.y - c.y) - fz2 * (a.y - b.y)) / fm1; // x0 Y = (fz1 * (a.x - c.x) - fz2 * (a.x - b.x)) / fm2; // y0 } vector<pair<double,double>> mpp; int main() { int n; scanf("%d", &n); for (int i = 1; i <= n; i++) scanf("%lf%lf", &a[i].x, &a[i].y); for (int i = 1; i <= n; i++){ for (int j = i + 1; j <= n; j++){ solve({0, 0}, a[i], a[j]); if (X == Y && sgn(X-1e18) == 0) continue; mpp.push_back({X,Y}); } } if(mpp.size()==0){ putchar('1'); return 0; } sort(mpp.begin(),mpp.end()); int ma = 1; int num = 1; pair<double,double> now=mpp[0]; for(int i=1;i<mpp.size();i++){ if(mpp[i]==now) ++num; else{ now=mpp[i]; ma=max(ma,num); num=1; } ma=max(ma,num); } for (int i = 1; i <= n; i++){ if (i * (i - 1) == ma * 2){ printf("%d ", i); return 0; } } return 0; }


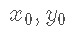 有唯一解的条件是系数行列式不为 0 :
有唯一解的条件是系数行列式不为 0 :


 支付宝扫一扫
支付宝扫一扫 微信扫一扫
微信扫一扫










最新评论