內插是数学领域数值分析中的通过已知的离散数据求未知数据的过程或方法。

根据若干离散的数据数据，得到一个连续的函数（也就是曲线）或者更加密集的离散方程与已知数据相吻合。这个过程叫做拟合。內插是曲线必须通过已知点的拟合。

1.线性插值

　　已知坐标 (x0, y0) 与 (x1, y1)，要得到 [x0, x1] 区间内某一位置 x 在直线上的值。

　　

　　由于 x 值已知，所以可以从公式得到 y 的值

　　

　　已知 y 求 x 的过程与以上过程相同，只是 x 与 y 要进行交换。

　　例如，

　　原来的数值序列：0，10，20，30，40 
　　线性插值一次为：0，5，10，15，20，25，30，35，40 
　　即认为其变化（增减）是线形的，可以在坐标图上画出一条直线 。

　　线性插值经常用于补充表格中的间隔部分。

　　两值之间的线性插值基本运算在计算机图形学中的应用非常普遍，以至于在计算机图形学领域的行话中人们将它称为 lerp。所有当今计算机图形处理器的硬件中都集成了线性插值运算，并且经常用来组成更为复杂的运算：

　　例如，可以通过三步线性插值完成一次双线性插值运算。由于这种运算成本较低，所以对于没有足够数量条目的光滑函数来说，它是实现精确快速查找表的一种非常好的方法。

　　在一些要求较高的场合，线性插值经常无法满足要求。在这种场合，可以使用多项式插值或者样条插值来代替。

　　线性插值可以扩展到有两个变量的函数的双线性插值。

　　双线性插值经常作为一种粗略的抗混叠滤波器使用，三线性插值用于三个变量的函数的插值。线性插值的其它扩展形势可以用于三角形与四面体等其它类型的网格运算。

 

 

2.双线性插值

 

　　在地球物理中，会经常用到双线性插值（Bilinear interpolation）。比

　　如，模拟生成的地表均匀网格上的速度场或者同震位移场。要与GPS观测点上的观测同震位移场进行比较。就必须将均匀网格点的值插值到GPS太站上。这就需要用到双线性插值。

 

双线性插值。

 

In mathematics, bilinear interpolation is an extension of linear interpolation for interpolating functions of two variables(e.g, x andy) on a regular grid. The interpolated function should not use the term of x² or y², but xy, which is the bilinear form of x and y.

 

　　其核心思想是在两个方向分别进行一次线性插值。

 

　　Thekey idea is to perform linear interpolation first in one direction, and then again in the other direction.Although each step is linear in the sampled values and in the position, the interpolation as a whole is not linear but rather quadratic in the sample location (details below).

 

　　

 

　　红色的数据点与待插值得到的绿色点

 

　　假如我们想得到未知函数 f 在点 P = (x, y) 的值，假设我们已知函数 f 在 Q11 = (x1, y1)、Q12 = (x1, y2), Q21 = (x2, y1) 以及 Q22 = (x2, y2) 四个点的值。

 

首先在 x 方向进行线性插值，得到

 

 

然后在 y 方向进行线性插值，得到

 

 

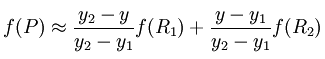
这样就得到所要的结果 f(x, y)，

 

 

如果选择一个坐标系统使得 f 的四个已知点坐标分别为 (0, 0)、(0, 1)、(1, 0) 和 (1, 1)，那么插值公式就可以化简为

 

 

或者用矩阵运算表示为

 

 

与这种插值方法名称不同的是，这种插值方法并不是线性的，它的形式是

 

 

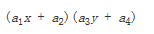
它是两个线性函数的乘积。看到了吧，双线性插值并不是线性。

 

Contrary to what the name suggests, the bilinear interpolant is not linear

 

 

另外，插值也可以表示为

 

 

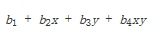
对于单位正方形，

 

 

在这两种情况下，常数的数目都对应于给定的 f 的数据点数目。

 

线性插值的结果与插值的顺序无关。首先进行 y 方向的插值，然后进行 x 方向的插值，所得到的结果是一样的。

 

双线性插值的一个显然的三维空间延伸是三线性插值。

3.三线性插值

　　三线性插值是在三维离散采样数据的张量积网格上进行线性插值的方法。

　　这个张量积网格可能在每一维度上都有任意不重叠的网格点，但并不是三角化的有限元分析网格。这种方法通过网格上数据点在局部的矩形棱柱上线性地近似计算点 (x,y,z) 的值。 

三线性插值在一次n=1三维D=3(双线性插值的维数：D=2，线性插值：D=1)的参数空间中进行运算，这样需要(1 + n)^D = 8个与所需插值点相邻的数据点。
三线性插值等同于三维张量的一阶B样条插值。
三线性插值运算是三个线性插值运算的张量积。

　　实例

　　在一个步距为1的周期性立方网格上，取x_d,y_d,z_d　为待计算点，距离小于　x,y,z,　的最大整数的差值，即，

　　

　　首先沿着z轴插值，得到：

　　

　　然后，沿着y轴插值，得到：

　　w₁ = i₁(1 − y_d) + i₂y_d

　　w₂ = j₁(1 − y_d) + j₂y_d

　　最后，沿着x轴插值，得到：

　　IV = w₁(1 − x_d) + w₂x_d
　　这样就得到该点的预测值。

　　三线性插值的结果与插值计算的顺序没有关系，也就是说，按照另外一种维数顺序进行插值，例如沿着 x、 y、z 顺序插值将会得到同样的结果。这也与张量积的交换律完全一致。

4.  双线性插值算法性能效果优化

 　　一般用在二维图像插值领域

　　假设源图像大小为mxn，目标图像为axb。那么两幅图像的边长比分别为：m/a和n/b。注意，通常这个比例不是整数，编程存储的时候要用浮点型。

　　目标图像的第（i,j）个像素点（i行j列）可以通过边长比对应回源图像。其对应坐标为（i*m/a,j*n/b）。显然，这个对应坐标一般来说不是整数，而非整数的坐标是无法在图像这种离散数据上使用的。

　　双线性插值通过寻找距离这个对应坐标最近的四个像素点，来计算该点的值（灰度值或者RGB值）。

　　如果你的对应坐标是（2.5,4.5），那么最近的四个像素是（2，4）、（2，5）、（3，4），（3，5）。

　　若图像为灰度图像，那么（i，j）点的灰度值可以通过一下公式计算：

　　f(i,j)=w1*p1+w2*p2+w3*p3+w4*p4;

　　其中，pi(i=1,2,3,4)为最近的四个像素点，wi(i=1,2,3,4)为各点相应权值。关于权值的计算，在维基百科和百度百科上写的很明白。

存在的问题

 

　　这部分的前提是，你已经明白什么是双线性插值并且在给定源图像和目标图像尺寸的情况下，可以用笔计算出目标图像某个像素点的值。

　　当然，最好的情况是你已经用某种语言实现了网上一大堆博客上原创或转载的双线性插值算法，然后发现计算出来的结果和matlab、openCV对应的resize（）函数得到的结果完全不一样。

 

　　那这个究竟是怎么回事呢？

 

　　其实答案很简单，就是坐标系的选择问题，或者说源图像和目标图像之间的对应问题。

 

　　按照网上一些博客上写的，源图像和目标图像的原点（0，0）均选择左上角，然后根据插值公式计算目标图像每点像素，假设你需要将一幅5×5的图像缩小成3×3，那么源图像和目标图像各个像素之间的对应关系如下：

 

　　

　　只画了一行，用做示意，从图中可以很明显的看到，如果选择左上角为原点（0，0），那么最右边和最下边的像素实际上并没有参与计算，而且目标图像的每个像素点计算出的灰度值也相对于源图像偏左偏上。

 只要在计算对应坐标的时候改为以下公式即可，

int x=(i+0.5)*m/a-0.5

int y=(j+0.5)*n/b-0.5 ，instead of 

int x=i*m/a

int y=j*n/b

利用上述公式，将得到正确的双线性插值结果

总结：

总结一下，我得到的教训有这么几条。

1.网上的一些资料有的时候并不靠谱，自己还是要多做实验。

2.不要小瞧一些简单的、基本的算法，让你写你未必会写，而且其中可能还藏着一些玄妙。

3.要多动手编程，多体会算法，多看大牛写的源码（虽然有的时候很吃力，但是要坚持看）。

　　在图像处理中，双线性插值算法的使用频率相当高，比如在图像的缩放中，在所有的扭曲算法中，都可以利用该算法改进处理的视觉效果。

　　

　　  用一个简单的数学表达式可以表示如下：

     f（x,y)=f(0,0)(1-x)(1-y)+f(1,0)x(1-y)+f(0,1)(1-x)y+f(1,1)xy

     合并有关项，可写为： f（x,y)=(  f(0,0)(1-x）+ f(1,0) x  ) (1-y)  +  (  f(0,1)(1-x)  +  f(1,1)x  )  y

     由上式可以看出，这个过程存在着大量的浮点数运算，对于图像这样大的计算用户来说，是一个较为耗时的过程。

 　　考虑到图像的特殊性，他的像素值的计算结果需要落在0到255之间，最多只有256种结果，由上式可以看出，一般情况下，计算出的f(x,y)是个浮点数，我们还需要对该浮点数进行取整。

　　因此，我们可以考虑将该过程中的所有类似于1-x、1-y的变量放大合适的倍数，得到对应的整数，最后再除以一个合适的整数作为插值的结果。

 　如何取这个合适的放大倍数呢，要从三个方面考虑，

第一：精度问题，如果这个数取得过小，那么经过计算后可能会导致结果出现较大的误差。

第二，这个数不能太大，太大会导致计算过程超过长整形所能表达的范围。

第三：速度考虑。假如放大倍数取为12，那么算式在最后的结果中应该需要除以12*12=144，但是如果取为16，则最后的除数为16*16=256，这个数字好，我们可以用右移来实现，而右移要比普通的整除快多了。

 　　综合考虑上述三条，我们选择2048这个数比较合适。

 

NewX = Int(PosX)                        '向下取整,NewX=25
NewY = Int(PosY)                        '向下取整,NewY=58PartX = (PosX - NewX) * 2048            '对应表达式中的X
PartY = (PosY - NewY) * 2048            '对应表达式中的Y
InvX = 2048 - PartX                     '对应表达式中的1-X
InvY = 2048 - PartY                     '对应表达式中的1-Y

Index1 = SamStride * NewY + NewX * 3    '计算取样点左上角邻近的那个像素点的内存地址
 Index2 = Index1 + SamStride 　　　　     '左下角像素点地址
ImageData(Speed + 2) = ((Sample(Index1 + 2) * InvX + Sample(Index1 + 5) * PartX) * InvY + (Sample(Index2 + 2) * InvX + 
                          Sample(Index2 + 5) * PartX) * PartY)  4194304       '处理红色分量
ImageData(Speed + 1) = ((Sample(Index1 + 1) * InvX + Sample(Index1 + 4) * PartX) * InvY + (Sample(Index2 + 1) * InvX +
                          Sample(Index2 + 4) * PartX) * PartY)  4194304       '处理绿色分量
 ImageData(Speed) = ((Sample(Index1) * InvX + Sample(Index1 + 3) * PartX) * InvY + (Sample(Index2) * InvX +
                      Sample(Index2 + 3) * PartX) * PartY)  4194304           '处理蓝色分量

　　以上代码中涉及到的变量都为整型（PosX及PosY当然为浮点型）。

      代码中Sample数组保存了从中取样的图像数据，SamStride为该图像的扫描行大小。

      观察上述代码，除了有2句涉及到了浮点计算，其他都是整数之间的运算。

      在Basic语言中，编译时如果勾选所有的高级优化，则 4194304会被编译为>>22，即右移22位，如果使用的是C语言，则直接写为>>22。

      需要注意的是，在进行这代代码前，需要保证PosX以及PosY在合理的范围内，即不能超出取样图像的宽度和高度范围。

      通过这样的改进，速度较直接用浮点类型快至少100%以上，而处理后的效果基本没有什么区别。

 

endl;